|
STX B+ Tree Template Classes 0.8.6
|
|
STX B+ Tree Template Classes 0.8.6
|
The B+ tree source package contains a speedtest program which compares the libstdc++ STL red-black tree with the implemented B+ tree with many different parameters. The newer STL hash table container from the __gnu_cxx namespace is also tested against the two trees. To keep focus on the algorithms and reduce data copying the multiset specializations were chosen. Note that the comparison between hash table and trees is somewhat unfair, because the hash table does not keep the keys sorted, and thus cannot be used for all applications.
Three set of test procedures are used: the first only inserts n random integers into the tree / hash table. The second test first inserts n random integers, then performs n lookups for those integers and finally erases all n integers. The last test only performs n lookups on a tree pre-filled with n integers. All lookups are successful.
These three test sequences are preformed for n from 125 to 4,096,000 or 32,768,000 where n is doubled after each test run. For each n the test procedure is repeated until at least one second execution time elapses during the repeated cycle. This way the measured speed for small n is averaged over up to 65,536 repetitions.
Lastly, it is purpose of the test to determine a good node size for the B+ tree. Therefore the test runs are performed on different slot sizes; both inner and leaf nodes hold the same number of items. The number of slots tested ranges from 4 to 256 slots and therefore yields node sizes from about 50 to 2,048 bytes. This requires that the B+ tree template is instantiated for each of the probed node sizes! In the 2011 test, only every other slot size is actually tested.
Two test results are included in the package: one done in 2007 with version 0.7 and another done in 2011 with version 0.8.6.
The speed test source code was compiled with g++ 4.1.2 -O3 -fomit-frame-pointer
Some non-exhaustive tests with the Intel C++ Compiler showed drastically different results. It optimized the B+ tree algorithms much better than gcc. More work is needed to get g++ to optimize as well as icc.
The results are be displayed below using gnuplot. All tests were run on a Pentium4 3.2 GHz with 2 GB RAM. A high-resolution PDF plot of the following images can be found in the package at speedtest/results-2007/speedtest.pdf
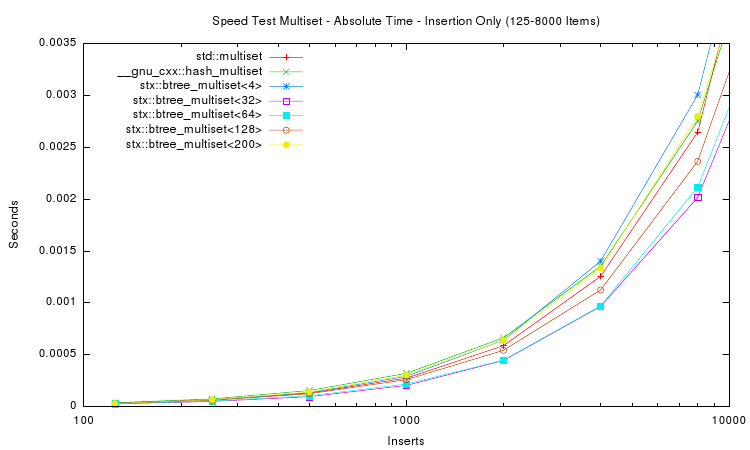
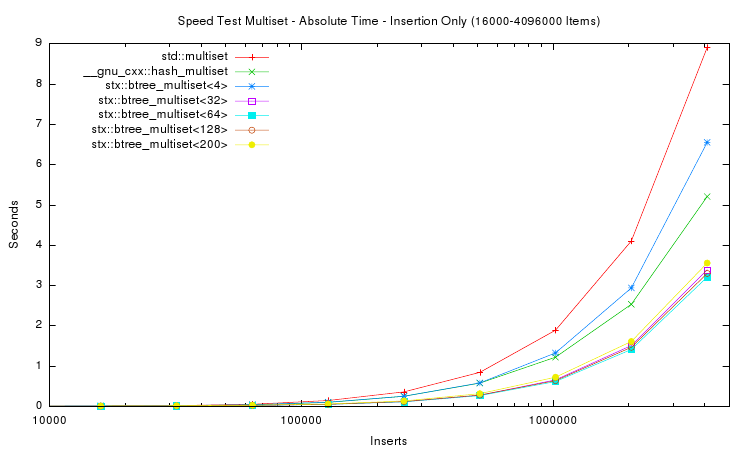
The first two plots above show the absolute time measured for inserting n items into seven different tree variants. For small n (the first plot) the speed of red-black tree and B+ tree are very similar. For large n the red-black tree slows down, and for n > 1,024,000 items the red-black tree requires almost twice as much time as a B+ tree with 32 slots. The STL hash table performs better than the STL map but not as good as the B+ tree implementations with higher slot counts.
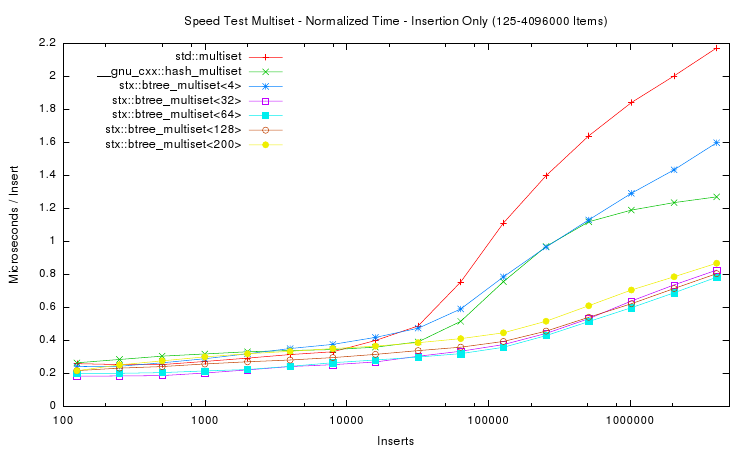
The next plot shows the insertion time per item, which is calculated by dividing the absolute time by the number of inserted items. Notice that insertion time is now in microseconds. The plot shows that the red-black tree reaches some limitation at about n = 16,000 items. Beyond this item count the B+ tree (with 32 slots) performs much better than the STL multiset. The STL hash table resizes itself in defined intervals, which leads to non-linearly increasing insert times.
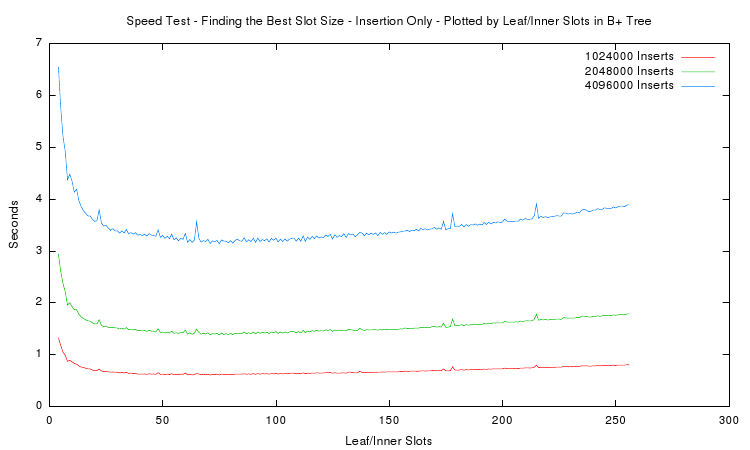
The last plots goal is to find the best node size for the B+ tree. It displays the total measured time of the insertion test depending on the number of slots in inner and leaf nodes. Only runs with more than 1 million inserted items are plotted. One can see that the minimum is around 65 slots for each of the curves. However to reduce unused memory in the nodes the most practical slot size is around 35. This amounts to total node sizes of about 280 bytes. Thus in the implementation a target size of 256 bytes was chosen.
The following two plots show the same aspects as above, except that not only insertion time was measured. Instead in the first plot a whole insert/find/delete cycle was performed and measured. The second plot is restricted to the lookup / find part.
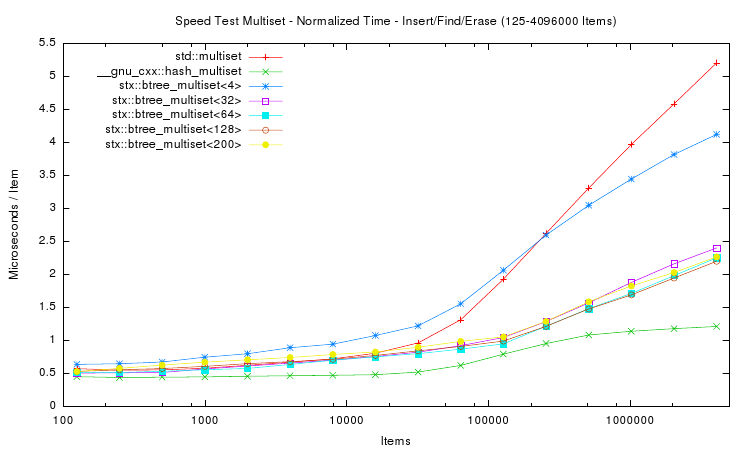
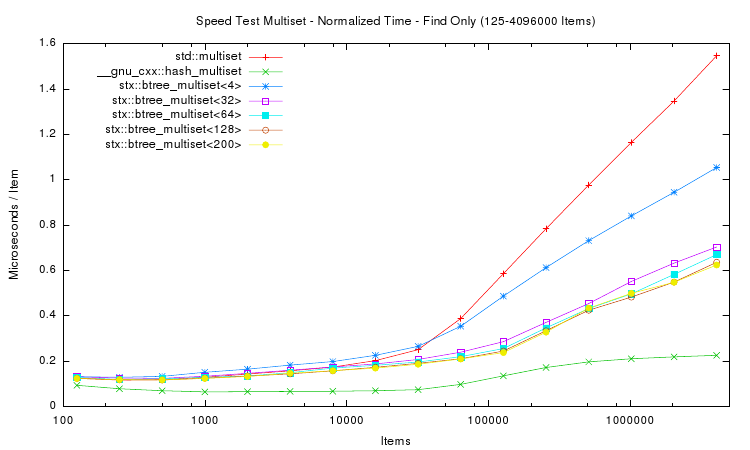
The results for the trees are in general accordance to those of only insertion. However the hash table implementation performs much faster in both tests. This is expected, because hash table lookup (and deletion) requires fewer memory accesses than tree traversal. Thus a hash table implementation will always be faster than trees. But of course hash tables do not store items in sorted order. Interestingly the hash table's performance is not linear in the number of items: it's peak performance is not with small number of items, but with around 10,000 items. And for item counts larger than 100,000 the hash table slows down: lookup time more than doubles. However, after doubling, the lookup time does not change much: lookup on tables with 1 million items takes approximately the same time as with 4 million items.
In 2011, after some smaller patches and fixes to the main code, I decided to rerun the old speed test on my new hardware and with up-to-date compilers.
The speedtest source code was compiled on a x86_64 architecture using gcc 4.4.5 with flags -O3 -fomit-frame-pointer. It was run in an Intel Core i7 950 clocked at 3,07 GHz. According to cpuinfo, this processor contains 8 MB L2 cache.
The full results of the newly run tests are found in the package at speedtest/results-2011/speedtest.pdf
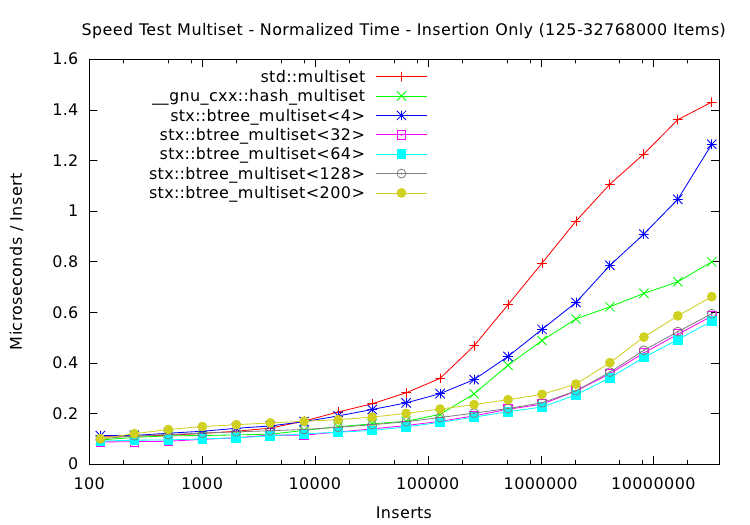
This plot is maybe the most interesting, especially compared with the old run from 2007. Again the B+ tree multiset implementation is faster than the red-black tree for large number of items in the tree. However, due to the faster hardware and larger cache sizes, the average insertion speed plots diverge notable at around 100,000 items instead of at 16,000 items for the older Pentium 4 CPU. Nevertheless, the graphs diverge for larger n in approximately the same fashion as in the older plots.
This lets one assume that the basic cache hierarchy architecture has not changed and the B+ tree implementation still works much better for larger item counts than the red-black tree.
 1.7.3
1.7.3