PolynomialStandard< Numeric > Class Template Reference

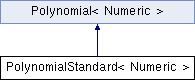
Represents a polynomial in standard monomial base. More...

Inheritance diagram for PolynomialStandard< Numeric >:

List of all members.

Public Member Functions
	PolynomialStandard ()
	PolynomialStandard (const std::vector< Numeric > &coefficient)
	PolynomialStandard (Numeric factor, const std::vector< Numeric > &roots)
	Construct polynomial from roots and a scaling multiplier.
unsigned int	degree () const
	Return degree of the polynomial.
Numeric	coefficient (unsigned int i) const
	Return a monomial coefficient.
std::string	toString (const std::string &X="X") const
	Return polynomial as latex math string.
std::string	toStringPlot () const
	Return polynomial as string for plotting with gnuplot.
Numeric	evaluate (Numeric X) const
	Calculate polynomial's value at the position X using Horner's schema.
std::vector< Numeric >	findRoots () const
	Calculate all real roots for a quadratic or cubic polynomial using the p-q- or Cardano's formulas.
PolynomialStandard	scale (Numeric alpha, Numeric beta) const
	Apply the linear transformation "X * (beta - alpha) + alpha" to the polynomial.
class PolynomialBezier< Numeric >	toBezier () const
	Convert the polynomial from standard base to the Bernstein-Bezier basis in the unit interval.
Private Attributes
std::vector< Numeric >	m_coefficient
	Coefficients of the polynomial. Degree is m_coefficients.size()-1.

---

Detailed Description

template<typename Numeric>
class PolynomialStandard< Numeric >

Represents a polynomial in standard monomial base.

Definition at line 786 of file clipper.cc.

---

Constructor & Destructor Documentation

template<typename Numeric>

PolynomialStandard< Numeric >::PolynomialStandard

(

)

[inline]

Definition at line 794 of file clipper.cc.

template<typename Numeric>

PolynomialStandard< Numeric >::PolynomialStandard

(

const std::vector< Numeric > &

coefficient

)

[inline, explicit]

Definition at line 798 of file clipper.cc.

template<typename Numeric>

PolynomialStandard< Numeric >::PolynomialStandard	(	Numeric	factor,
		const std::vector< Numeric > &	roots
	)		[inline]

Construct polynomial from roots and a scaling multiplier.

Definition at line 804 of file clipper.cc.

---

Member Function Documentation

template<typename Numeric>

Numeric PolynomialStandard< Numeric >::coefficient

(

unsigned int

i

)

const [inline]

Return a monomial coefficient.

Definition at line 858 of file clipper.cc.

template<typename Numeric>

unsigned int PolynomialStandard< Numeric >::degree

(

)

const [inline]

Return degree of the polynomial.

Definition at line 852 of file clipper.cc.

template<typename Numeric>

Numeric PolynomialStandard< Numeric >::evaluate

(

Numeric

X

)

const [inline]

Calculate polynomial's value at the position X using Horner's schema.

Definition at line 913 of file clipper.cc.

template<typename Numeric>

std::vector<Numeric> PolynomialStandard< Numeric >::findRoots

(

)

const [inline]

Calculate all real roots for a quadratic or cubic polynomial using the p-q- or Cardano's formulas.

Definition at line 926 of file clipper.cc.

template<typename Numeric>

PolynomialStandard PolynomialStandard< Numeric >::scale	(	Numeric	alpha,
		Numeric	beta
	)		const [inline]

Apply the linear transformation "X * (beta - alpha) + alpha" to the polynomial.

This remaps the interval [alpha,beta] to [0,1].

Definition at line 1033 of file clipper.cc.

template<typename Numeric >

PolynomialBezier< Numeric > PolynomialStandard< Numeric >::toBezier

(

)

const

Convert the polynomial from standard base to the Bernstein-Bezier basis in the unit interval.

Convert the polynomial from monomial representation to the Bernstein-Bezier basis in the unit interval.

Use scale() to transform the coefficients before applying this base conversion.

Definition at line 1429 of file clipper.cc.

template<typename Numeric>

std::string PolynomialStandard< Numeric >::toString

(

const std::string &

X = "X"

)

const [inline]

Return polynomial as latex math string.

Definition at line 865 of file clipper.cc.

template<typename Numeric>

std::string PolynomialStandard< Numeric >::toStringPlot

(

)

const [inline]

Return polynomial as string for plotting with gnuplot.

Definition at line 890 of file clipper.cc.

---

Member Data Documentation

template<typename Numeric>

std::vector<Numeric> PolynomialStandard< Numeric >::m_coefficient [private]

Coefficients of the polynomial. Degree is m_coefficients.size()-1.

Definition at line 791 of file clipper.cc.

---

The documentation for this class was generated from the following file:

• clipper.cc